Symmetry-adapted tensor

This example shows how to calculate irreps of crystallographic point groups and construct projection operator on identity representation. We apply the projection operator to obtaining symmetry-adapted tensor (e.g. elastic constant).

Import modules

from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from spglib import get_symmetry_from_database

import spgrep
from spgrep import get_crystallographic_pointgroup_irreps_from_symmetry
from spgrep.group import get_cayley_table
from spgrep.representation import is_representation, project_to_irrep
from spgrep.tensor import get_symmetry_adapted_tensors, apply_intrinsic_symmetry

print(f"spgrep=={spgrep.__version__}")

spgrep==0.3.4.dev177+gd763494

sns.set_context("poster")

Prepare point-group operations and representation

We consider crystallographic point group \(m\overline{3}m\).

# Pm-3m (No. 221)
symmetry = get_symmetry_from_database(hall_number=517)
rotations = symmetry["rotations"]  # (48, 3, 3)

Then, we define basis of strain tensors in Voigt order:

\[\begin{split}\mathbf{E}_{1} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}, \mathbf{E}_{2} = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}, \mathbf{E}_{3} = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}, \mathbf{E}_{4} = \frac{1}{\sqrt{2}} \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}, \mathbf{E}_{5} = \frac{1}{\sqrt{2}} \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}, \mathbf{E}_{6} = \frac{1}{\sqrt{2}} \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}.\end{split}\]

A rotation \(R\) in point group \(\mathcal{P}\) acts the basis of strain tensors as

\[R \mathbf{E}_{j} := \mathbf{R} \mathbf{E}_{j} \mathbf{R}^{\top} \quad (R \in \mathcal{P}),\]

where \(\mathbf{R}\) is a matrix representation of rotation \(R\). We define a representation matrix for this action as

\[R \mathbf{E}_{j} = \sum_{i=1}^{6} \mathbf{E}_{i} \Gamma_{ij}(R).\]

def get_standard_basis() -> list[np.ndarray]:
    # Basis for symmetric matrix in Voigt order (xx, yy, zz, yz, zx, xy)
    basis = [
        np.array(
            [
                [1, 0, 0],
                [0, 0, 0],
                [0, 0, 0],
            ],
            dtype=np.float64,
        ),
        np.array(
            [
                [0, 0, 0],
                [0, 1, 0],
                [0, 0, 0],
            ],
            dtype=np.float64,
        ),
        np.array(
            [
                [0, 0, 0],
                [0, 0, 0],
                [0, 0, 1],
            ],
            dtype=np.float64,
        ),
        np.array(
            [
                [0, 0, 0],
                [0, 0, 1],
                [0, 1, 0],
            ],
            dtype=np.float64,
        )
        / np.sqrt(2),
        np.array(
            [
                [0, 0, 1],
                [0, 0, 0],
                [1, 0, 0],
            ],
            dtype=np.float64,
        )
        / np.sqrt(2),
        np.array(
            [
                [0, 1, 0],
                [1, 0, 0],
                [0, 0, 0],
            ],
            dtype=np.float64,
        )
        / np.sqrt(2),
    ]
    return basis


def get_representation_on_symmetric_matrix(rotations: np.ndarray) -> np.ndarray:
    # take [e_{1,1}, e_{2,2}, e_{3,3}, e_{2,3}, e_{3,1}, e_{1,2}] as basis
    basis = get_standard_basis()
    rep = np.zeros((len(rotations), len(basis), len(basis)))
    for pos, rotation in enumerate(rotations):
        for j, bj in enumerate(basis):
            # operated = rotation.T @ bj @ rotation
            operated = rotation @ bj @ rotation.T
            for i, bi in enumerate(basis):
                rep[pos, i, j] = np.sum(operated * bi) / np.sum(bi * bi)

    # Sanity check if `rep` satisfy property of representation
    table = get_cayley_table(rotations)
    assert is_representation(rep, table)

    return rep


rep = get_representation_on_symmetric_matrix(rotations)

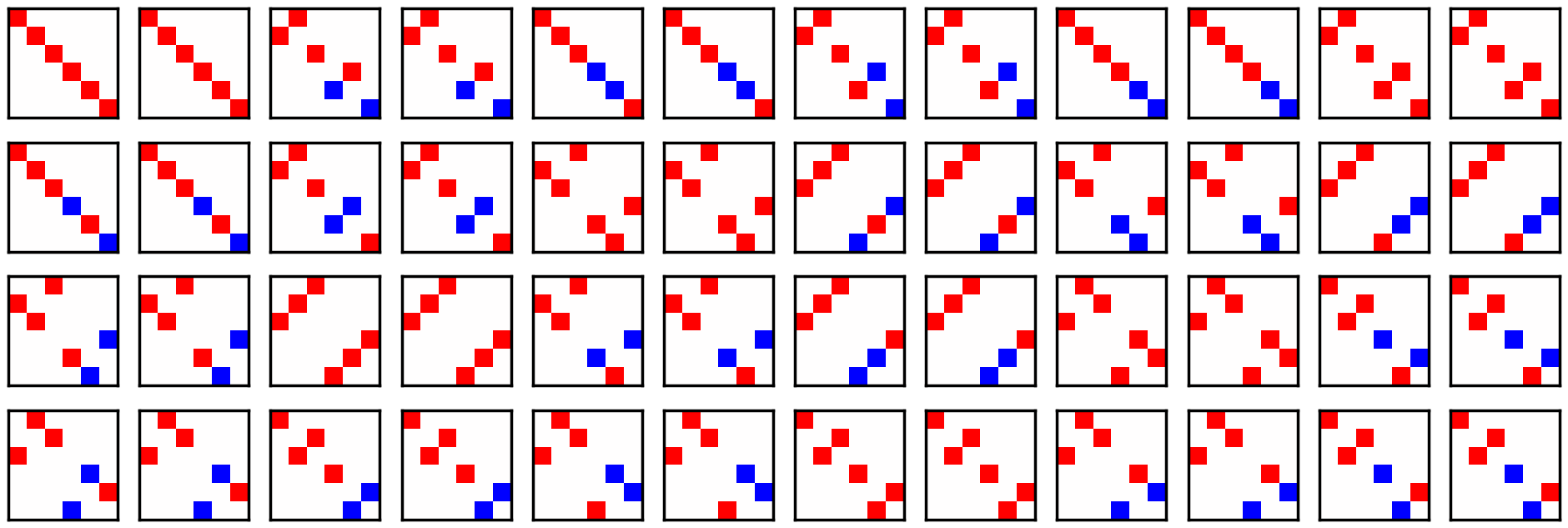
Of course, the representation matrices are not block-diagonalized:

nrows = 4
ncols = 12
fig, axes = plt.subplots(nrows, ncols, figsize=(2 * ncols, 2 * nrows))
for row in range(nrows):
    for col in range(ncols):
        idx = row * ncols + col
        ax = axes[row][col]
        ax.imshow(rep[idx], cmap="bwr", vmin=-1, vmax=1)
        ax.set_aspect("equal")
        ax.set_xticks([])
        ax.set_yticks([])

Calculate physically irreducible representation

For strain tensors, we need to consider representation over real number \(\mathbb{R}\). The spgrep.get_crystallographic_pointgroup_irreps_from_symmetry with real=True returns all unitary irreps over real number \(\mathbb{R}\) (also called as physically irreducible representation).

irreps = get_crystallographic_pointgroup_irreps_from_symmetry(rotations, real=True)

Basis functions for each irrep can be obtained by spgrep.representation.project_to_irrep:

all_basis = []
for irrep in irreps:
    list_basis = project_to_irrep(rep, irrep)
    for basis in list_basis:
        all_basis.append(basis)

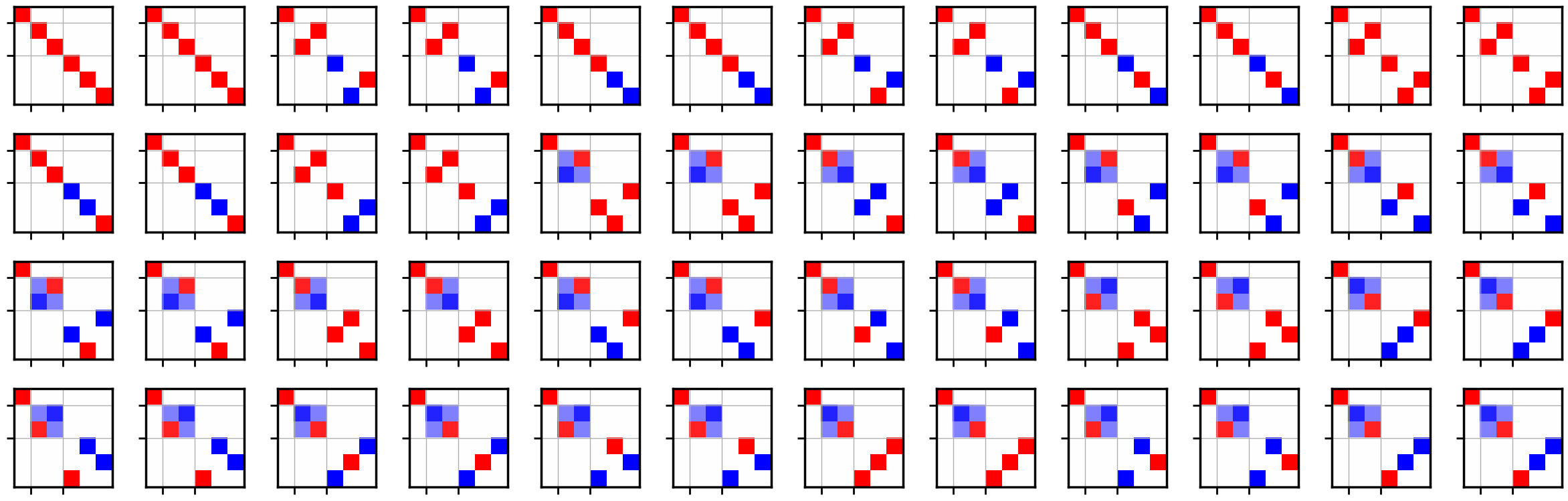
We can confirm the representation \(\Gamma\) is decomposed to three irreps: a one-dimensional, a two-dimensional, and a three-dimensional ones.

fig, axes = plt.subplots(nrows, ncols, figsize=(2 * ncols, 2 * nrows))
for row in range(nrows):
    for col in range(ncols):
        idx = row * ncols + col
        ax = axes[row][col]
        rep_transformed = np.concatenate(all_basis) @ rep[idx] @ np.concatenate(all_basis).T
        ax.imshow(rep_transformed, cmap="bwr", vmin=-1, vmax=1, aspect="equal")
        ax.set_xticks([])
        ax.set_yticks([])

        ax.set_xticks([0.5, 2.5], minor=True)
        ax.set_yticks([0.5, 2.5], minor=True)
        ax.grid(which="minor", linewidth=1)

plt.tight_layout()

Calculate symmetry-adapted tensors

expects = [1, 3, 6, 11]
for rank, expect in zip(range(1, len(expects) + 1), expects):
    tensors = get_symmetry_adapted_tensors(rep, rotations, rank, real=True)
    sym_tensors = apply_intrinsic_symmetry(tensors)
    print(f"Rank={rank}: {len(sym_tensors)}")
    assert len(sym_tensors) == expect

Rank=1: 1
Rank=2: 3
Rank=3: 6
Rank=4: 11