Application of space-group irreps to lattice vibration

This example shows how to prepare representation matrix of atomic displacements by space group, and block-diagonalize dynamical matrix for harmonic lattice vibration only from symmetry.

Import modules

from pathlib import Path

import phonopy
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

import spgrep
from spgrep import get_spacegroup_irreps
from spgrep.representation import check_spacegroup_representation, project_to_irrep

print(f"spgrep=={spgrep.__version__}")

spgrep==0.3.4.dev177+gd763494

sns.set_context("poster")

Prepare space-group operations and representation

We consider lattice vibration of Perovskite structure (\(Pm\overline{3}m\)) at X point.

# Perovskite structure: Pm-3m (No. 221)
a = 3.986
lattice = np.array(
    [
        [a, 0, 0],
        [0, a, 0],
        [0, 0, a],
    ]
)
positions = np.array(
    [
        [0, 0.5, 0.5],  # O(3c)
        [0.5, 0, 0.5],  # O(3c)
        [0.5, 0.5, 0],  # O(3c)
        [0.5, 0.5, 0.5],  # Ti(1b)
        [0, 0, 0],  # Ba(1a)
    ]
)
numbers = [0, 0, 0, 1, 2]

qpoint = [0.5, 0, 0]  # X point (with primitive cell)

Irreps of the space group is obtained by spgrep.get_spacegroup_irreps:

irreps, rotations, translations, mapping_little_group = get_spacegroup_irreps(
    lattice, positions, numbers, qpoint
)

# Sanity check if `irreps` are representation for space group
little_rotations = rotations[mapping_little_group]
little_translations = translations[mapping_little_group]
for irrep in irreps:
    assert check_spacegroup_representation(little_rotations, little_translations, qpoint, irrep)

Let \(u_{\mu}(l \kappa)\) be a \(\mu\)-direction atomic displacement of the \(\kappa\)-th atom in the \(l\)-th unit cell. We consider the fourier transformation of \(u_{\mu}(l \kappa)\),

\[\mathbf{u}(\kappa; \mathbf{q}) := \sqrt{\frac{M_{\kappa}}{N}} \sum_{l} \mathbf{u}(\mathbf{r}(l\kappa)) e^{ i \mathbf{q} \cdot \mathbf{r}(l) },\]

where \(N\) is number of lattice points in a supercell, and \(M_{\kappa}\) is mass of the \(\kappa\)-th atom. Let \(\mathbf{r}(l\kappa)\) be equilibrium position of the \(\kappa\)-th atom in the \(l\)-th unit cell. The fourier transformation of \(u_{\mu}(l \kappa)\) forms representation of space group \(\mathcal{G}\) [1] as

\[g u_{\mu}(\kappa; \mathbf{q}) = \sum_{\kappa'\mu'} u_{\mu'}(\kappa'; \mathbf{R}_{g} \mathbf{q} ) \Gamma_{\kappa'\mu'; \kappa\mu}^{\mathbf{q}}(g) \quad (g \in \mathcal{G}),\]

where \(\mathbf{R}_{g}\) represents rotation part of \(g\), and

\[\Gamma_{\kappa'\mu'; \kappa\mu}^{\mathbf{q}}(g) := \exp \left( -i \mathbf{R}_{g} \mathbf{q} \cdot (g \mathbf{r}(0\kappa)) - \mathbf{r}(\mathbf{0}\,g\kappa) \right) [\mathbf{R}_{g}]_{\mu'\mu} \delta_{ g\kappa, \kappa' }.\]

[1]

1. 1. Maradudin and S. H. Vosko, Rev. Mod. Phys. 40, 1–37 (1968).

def get_displacements_representation(
    lattice,
    positions,
    little_rotations,
    little_translations,
    qpoint,
):
    r"""Compute representation matrix for fourier-transformed displacements.

    .. math::
       \\Gamma_{\\kappa'\\mu'; \\kappa\\mu}^{\\mathbf{q}}(g) := \\exp \\left( -i \\mathbf{R}_{g} \\mathbf{q} \\cdot \\mathbf{h}_{g}(\\kappa) \\right) [\\mathbf{R}_{g}]_{\\mu'\\mu} \\delta_{ g\\kappa, \\kappa' }
    """
    little_order = len(little_rotations)
    num_atoms = len(positions)

    # Operation-`i` moves atom-`kappa` to `permutations[i, kappa]`
    permutations = np.zeros((little_order, num_atoms), dtype=int)
    for i, (Ri, vi) in enumerate(zip(little_rotations, little_translations)):
        for kappa, position in enumerate(positions):
            new_pos = np.remainder(Ri @ position + vi, 1)
            for kappa2, position2 in enumerate(positions):
                if np.allclose(position2, new_pos):
                    permutations[i, kappa] = kappa2
                    break

    shifts = np.zeros((little_order, num_atoms, 3))
    for i, (Ri, vi) in enumerate(zip(little_rotations, little_translations)):
        perm_i = permutations[i]
        shifts[i] = positions @ Ri.T + vi[None, :] - positions[perm_i]

    perm_rep = np.zeros((little_order, num_atoms, num_atoms), dtype=np.complex128)
    for i, Ri in enumerate(little_rotations):
        for kappa in range(num_atoms):
            kappa2 = permutations[i, kappa]
            perm_rep[i, kappa2, kappa] = np.exp(
                -2j * np.pi * np.dot(Ri.T @ qpoint, shifts[i, kappa])
            )

    # Rotation matrix in cartesian (order, 3, 3)
    A = np.transpose(lattice)  # column-wise lattice vectors
    Ainv = np.linalg.inv(A)
    rotation_rep = np.array([A @ r @ Ainv for r in little_rotations], dtype=np.complex128)

    rep = np.einsum("ipq,iab->ipaqb", perm_rep, rotation_rep, optimize="greedy")
    return rep.reshape(-1, num_atoms * 3, num_atoms * 3)


rep = get_displacements_representation(
    lattice, positions, little_rotations, little_translations, qpoint
)

The order of the little co-group at X point is 16, and the atomic displacements are represented by 15 components (x,y,z directions for 5 atoms). Thus, shape of rep is (16, 15, 15).

rep.shape

(16, 15, 15)

nrows = 2
ncols = 8
fig, axes = plt.subplots(nrows, ncols, figsize=(2 * ncols, 2 * nrows))
for row in range(nrows):
    for col in range(ncols):
        idx = row * ncols + col
        ax = axes[row][col]
        ax.imshow(np.abs(rep[idx]), cmap="bwr", vmin=-1, vmax=1)
        ax.set_aspect("equal")
        ax.set_xticks([])
        ax.set_yticks([])

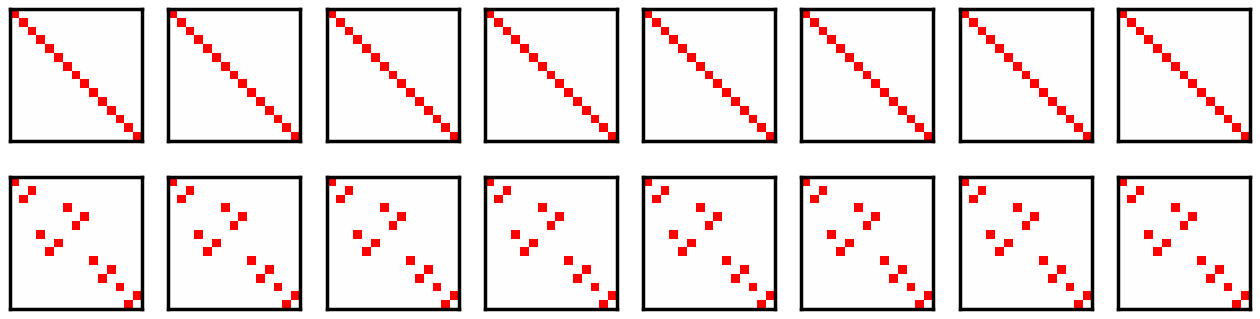
Load dynamical matrix from PhononDB

Next, we consider to construct a projection operator, and block-diagonalize dynamical matrix at X point. We use a phonon calculation of Perovskite-BaTiO3 in PhononDB.

# http://phonondb.mtl.kyoto-u.ac.jp/xz-files/phonopy_mp-2998.yaml.xz
path = Path().resolve().parent.parent / "examples" / "phonopy_mp-2998.yaml.xz"
ph = phonopy.load(path)
ph.dynamical_matrix.run(qpoint)
dynamical_matrix = ph.dynamical_matrix.dynamical_matrix

fig, ax = plt.subplots(figsize=(2 * ncols, 2 * nrows))
ax.imshow(np.abs(dynamical_matrix), cmap="bwr", vmin=-1.5, vmax=1.5)
ax.set_xticks([])
ax.set_yticks([])
plt.show()

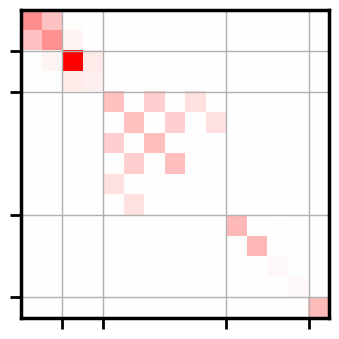
Apply projection operator and block-diagonalize dynamical matrix

all_basis = []
for irrep in irreps:
    list_basis = project_to_irrep(rep, irrep)
    print(f"{len(list_basis)} basis vectors for irrep with {irrep.shape}")
    all_basis.extend(list_basis)

blocked_dynamical_matrix = (
    np.concatenate(all_basis) @ dynamical_matrix @ np.conj(np.concatenate(all_basis)).T
)

fig, ax = plt.subplots(figsize=(2 * ncols, 2 * nrows))
ax.imshow(np.abs(blocked_dynamical_matrix), cmap="bwr", vmin=-1.5, vmax=1.5)
ax.set_xticks([])
ax.set_yticks([])
ax.set_xticks([1.5, 3.5, 9.5, 13.5], minor=True)
ax.set_yticks([1.5, 3.5, 9.5, 13.5], minor=True)
ax.grid(which="minor", linewidth=1)
plt.show()

2 basis vectors for irrep with (16, 1, 1)
0 basis vectors for irrep with (16, 1, 1)
0 basis vectors for irrep with (16, 1, 1)
2 basis vectors for irrep with (16, 1, 1)
3 basis vectors for irrep with (16, 2, 2)
2 basis vectors for irrep with (16, 2, 2)
1 basis vectors for irrep with (16, 1, 1)
0 basis vectors for irrep with (16, 1, 1)
0 basis vectors for irrep with (16, 1, 1)
0 basis vectors for irrep with (16, 1, 1)